What Does It Mean to Control Weather?
In recent years, the impacts of climate change have led to increasingly frequent weather-related disasters in Japan, such as typhoons and heavy rainfall. These disasters have had significant effects on society through human casualties and damage to infrastructure. Against this background, research on weather control—the deliberate intervention in atmospheric phenomena to reduce disaster impacts—has been actively pursued.
Weather control requires identifying appropriate interventions that guide future atmospheric states toward desirable outcomes. Such interventions are determined through weather intervention optimization. This refers to optimizing parameters such as the location and intensity of interventions in order to achieve control objectives, for example minimizing total precipitation. However, because atmospheric phenomena are extremely large-scale and complex, strict optimization is not realistic in practice. As a result, approximate methods, heuristic approaches, and sequential or local optimization techniques are required.
In weather control, the key questions are where to intervene, how strongly, and in what manner, in order to influence future weather in a desirable direction. These questions are formulated as weather intervention optimization problems, where parameters such as intervention location and strength are optimized to achieve control objectives like precipitation reduction. Due to the high dimensionality and complexity of atmospheric models, exact optimization is impractical, making approximate and heuristic optimization approaches essential.
As of March 2025, our research focuses on applying black-box optimization methods to weather intervention optimization problems. Black-box optimization refers to techniques that search for inputs that minimize or maximize an objective function using only input–output relationships, without requiring explicit mathematical expressions for the objective function or constraints. These methods do not rely on gradient information and can achieve relatively strong search performance with a limited number of simulations, making them well suited for computationally expensive weather simulations.
Specific Research Topics
In this research, we use SCALE-RM (SCALE-Regional Model), which is based on the numerical weather modeling framework SCALE (Scalable Computing for Advanced Library and Environment). The effects of interventions obtained through black-box optimization are evaluated using numerical simulations. Referring to the SCALE user guide and existing codes developed by senior researchers, we implement methods such as Bayesian optimization and particle swarm optimization, and compare their control performance, measured by the reduction in total precipitation.
Below, we introduce representative experimental settings that have been investigated so far.
Warm Bubble Experiment
The warm bubble experiment is an idealized setup designed to reproduce the initiation of convective clouds under simplified conditions. At the initial time, a warm air bubble is placed in the lower central region of the computational domain, triggering an updraft. As time progresses, cloud development and precipitation are numerically simulated.
The computational domain covers an area of approximately 10 km × 10 km horizontally and about 20 km vertically. This space is discretized into many grid cells, and atmospheric state variables in each cell are computed at fine time intervals to represent weather phenomena.
The video below shows the temporal evolution of precipitation intensity [mm/h] without intervention.

The figure below shows the accumulated precipitation over one hour.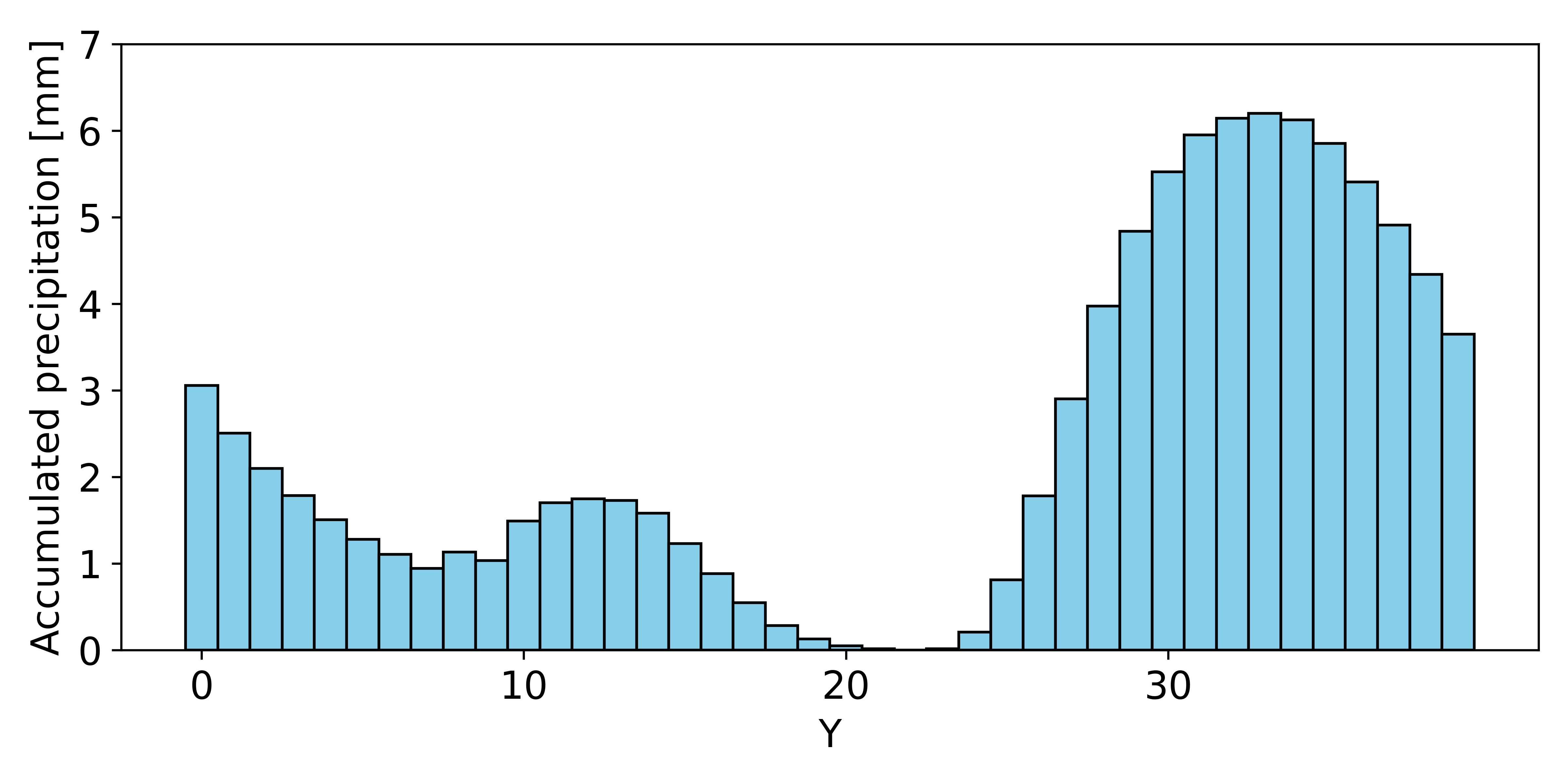
In this experimental setup, precipitation without intervention is used as a reference, and changes resulting from interventions applied to atmospheric state variables such as momentum and potential temperature are evaluated. Specifically, we consider a control problem in which interventions are applied to the momentum field at the initial time in order to reduce the accumulated precipitation over one hour. The intervention location and strength are represented by three variables, which are optimized using black-box optimization to minimize total accumulated precipitation over the domain. Under these conditions, particle swarm optimization achieved a maximum reduction of 43.6% in one-hour accumulated precipitation.

現実大気実験
In real-atmosphere experiments, initial conditions based on actual atmospheric states and surface conditions are used to reproduce real weather events. By appropriately selecting the initial time, it is possible to numerically simulate weather cases directly related to disasters, such as typhoons and heavy rainfall.
The video below shows the temporal evolution of precipitation intensity [mm/h] without intervention, where strong rainfall is observed over the Tohoku region and offshore of the Kanto region. In this study, we aim to mitigate heavy rainfall in the Tohoku region by applying interventions to the atmospheric momentum at the initial time. The control objective is to reduce the six-hour accumulated precipitation within the region indicated by the red box in the right panel of the figure. The intervention location and strength are determined by four variables, which are optimized using black-box optimization methods.

Under this experimental setup, Bayesian optimization and particle swarm optimization achieved a maximum reduction of 4.1% in six-hour accumulated precipitation in the heavy rainfall region.
Control Theory
Control theory, which provides a framework for guiding systems toward desirable states, plays an important role in weather control research. However, traditional control theory has primarily focused on relatively low-dimensional systems with clearly defined structures, and has not been designed to directly address large-scale and complex phenomena such as atmospheric dynamics.
To address this gap, our research incorporates data-driven approaches, including artificial intelligence techniques and ensemble forecasting, to extend the scope of conventional control theory. As of March 2025, we are particularly focusing on model predictive control and investigating its applicability to weather phenomena.
Concluding Remarks
This research is conducted as part of the Moonshot Research and Development Program, Goal 8: “A future free from concentrated heavy rainfall damage achieved through offshore heavy rainfall generation.” By approaching the challenging topic of weather control from the perspectives of computation, optimization, and control, we aim to explore new forms of research.
For more details about the project, please refer to the following websites.
A Message to Students
This research does not assume prior expertise in meteorology or control theory. Rather, having simple questions such as “What does this computation represent?” or “Why does changing the search method affect the result?” is an important starting point.
In practice, research involves repeatedly running numerical simulations, visualizing results, analyzing why certain approaches did not work, and refining experimental conditions. Using programming and algorithms to gradually explore large-scale and complex phenomena offers a distinctly information-science-oriented research experience.
Although the theme addresses socially important issues related to weather disasters, daily research activities consist of a sequence of computationally interesting questions, such as how to choose parameters or how different optimization methods affect outcomes. A key feature of this research is the ability to consider both social relevance and computational curiosity simultaneously.
Theoretical foundations and background knowledge required after joining the laboratory are learned step by step through the research process. For students who want to explore how programming, probability and statistics, and algorithms learned at the undergraduate level can be applied to real research problems, this topic provides a suitable entry point.
