什麼是氣象控制?
近年來,受氣候變遷影響,日本各地頻繁發生颱風與豪雨等氣象災害。這些災害透過人員傷亡與基礎設施破壞,對社會造成重大影響。在此背景下,以降低災害損失為目的,對氣象現象進行人為介入的「氣象控制」研究正逐步展開。
氣象控制的核心在於尋找能將未來大氣狀態引導至理想方向的適當介入方式。這些介入是透過「氣象介入最佳化」來求得的。所謂氣象介入最佳化,是指為了達成如降水量最小化等控制目標,對介入的位置與強度等參數進行最佳化。然而,由於氣象現象規模龐大且結構複雜,進行嚴格的最佳化在實務上並不現實,因此必須採用近似方法、啟發式方法,以及逐次或局部的最佳化技術。
在氣象控制中,必須思考「在哪裡」、「以何種程度」、「進行何種介入」,才能將未來的氣象現象引導至理想狀態。這些問題可被形式化為氣象介入最佳化問題,例如透過最佳化介入位置與強度來達成降水量最小化的目標。由於氣象模型維度極高且極為複雜,嚴格最佳化並不可行,因此近似與啟發式最佳化方法顯得尤為重要。
截至 2025 年 3 月,本研究著眼於黑箱最佳化方法,並將其應用於氣象介入最佳化問題。黑箱最佳化是指在無法明確表示評估函數與限制條件的情況下,僅利用輸入與輸出之間的對應關係,搜尋可使評估函數最小化或最大化的輸入。此類方法不需要梯度資訊,且在有限模擬次數下仍能展現良好的搜尋效能,因此被認為非常適合計算成本高昂的氣象模擬。
具體研究內容
本研究使用基於數值氣象模型 SCALE(Scalable Computing for Advanced Library and Environment)所建構的 SCALE-RM(SCALE-Regional Model),並透過黑箱最佳化所求得的介入方案,利用數值模擬來評估其效果。參考 SCALE 使用手冊與前人所撰寫的程式碼,我們實作了貝葉斯最佳化與粒子群最佳化等方法,並比較各方法在控制效果上的差異,例如總降水量的削減程度。
以下介紹目前為止所研究的代表性實驗設定。
Warm Bubble Experiment
Warm bubble experiment 是一種在理想化條件下,用以重現積雲對流生成過程的實驗設定。在初始時刻,於計算區域下方中央配置一團暖空氣,藉此觸發上升氣流,隨時間推移,雲的發展與降水過程會被數值模擬重現。
計算區域在水平方向約為 10 公里 × 10 公里,高度約 20 公里,並被劃分為大量網格單元。透過對每個網格單元中的大氣狀態變數進行細時間步長的計算,來表現氣象現象。
下方影片顯示在未進行介入時,降水強度 [mm/h] 隨時間的變化。

下方圖像則顯示一小時的累積降水量。
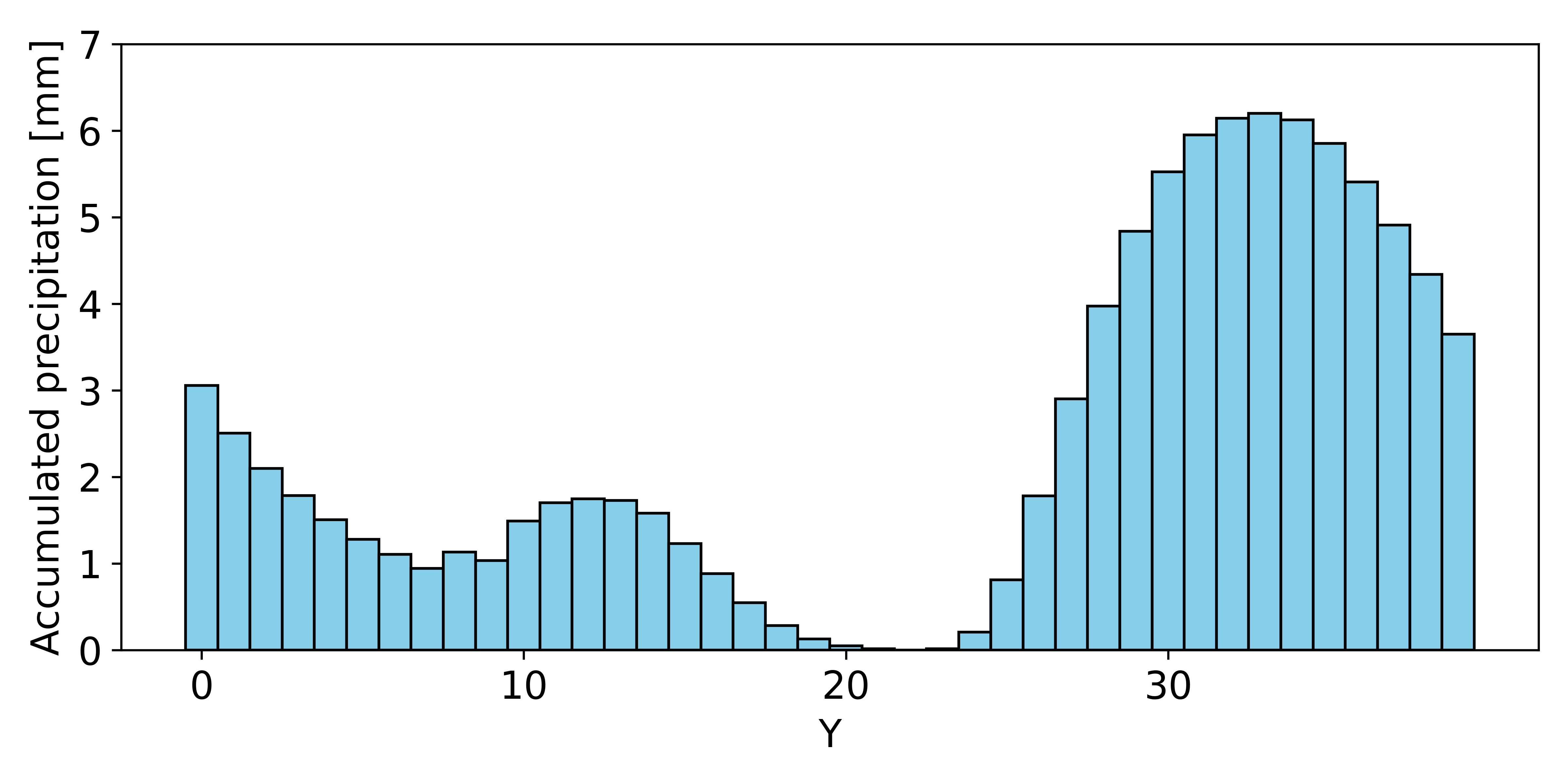
在此實驗設定中,以未介入時的降水分布作為基準,評估對大氣運動量與位溫等狀態變數進行介入後所產生的變化。具體而言,本研究考慮在初始時刻對運動量施加介入,以降低一小時內的累積降水量。介入的位置與強度以三個變數表示,並透過黑箱最佳化進行搜尋,以最小化整個計算區域的累積降水量。在此條件下,粒子群最佳化可將一小時降水量最多削減 43.6%。
現實大氣實驗
現實大氣實驗使用基於實際大氣狀態與地表條件的初始值,以重現真實的氣象現象。透過適當設定初始時刻,可數值模擬與颱風或豪雨等災害直接相關的氣象案例。
下方影片顯示在未介入情況下的降水強度 [mm/h] 隨時間變化,可觀察到東北地方與關東外海出現強降雨。本研究以減輕東北地方豪雨為目標,在初始時刻對大氣運動量進行介入,並考慮削減圖中紅框所示區域內六小時的累積降水量。此處以四個變數決定介入的位置與強度,並利用黑箱最佳化方法進行最佳化。

在此實驗設定下,貝葉斯最佳化或粒子群最佳化可將豪雨區域內六小時累積降水量最多削減 4.1%。
控制理論
在氣象控制研究中,引導系統朝向理想狀態的理論——控制理論——扮演著重要角色。然而,傳統控制理論主要針對低維度且結構明確的系統,並未假設能直接處理如氣象般的大規模與複雜現象。
因此,本研究引入人工智慧技術與集合預報等資料驅動方法,以擴展既有控制理論的適用範圍。截至 2025 年 3 月,我們特別關注模型預測控制,並持續探討其在氣象現象中的應用可能性。
結語
本研究作為「登月型研究開發事業」目標 8——「透過海上豪雨生成,實現擺脫集中豪雨災害的未來」——的一部分而進行。面對氣象控制這一具挑戰性的研究主題,我們嘗試從計算、最佳化與控制等資訊科學視角,探索新的研究形態。
更多關於本計畫的資訊,請參考以下網站。
給學生的話
本研究並不假設學生一開始就具備氣象或控制方面的專業知識。相反地,能提出「這個計算代表什麼?」或「為什麼改變搜尋方法會影響結果?」這樣的基本疑問,正是重要的起點。
實際研究中,會反覆執行數值模擬、將結果視覺化、分析未達預期的原因,並調整下一次的實驗條件。透過程式設計與演算法,一步步切入龐大而複雜的現象,是相當具有資訊科學特色的研究體驗。
研究主題雖然涉及氣象災害這一社會上極為重要的問題,但日常工作本身則充滿了「參數該如何選擇」、「搜尋方法會如何影響結果」等計算上引人入勝的問題。能同時思考社會意義與計算趣味性,是本研究的一大特色。
配屬後所需的理論與背景知識,會在研究過程中逐步學習。對於希望嘗試將大學階段所學的程式設計、機率統計與演算法知識應用於實際研究問題的學生而言,這是一個良好的研究題材。
